Differentiation is the process of finding the rate of change of a function. We have proven that if f is a variable dependent on an independent variable x, such that 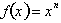 then
then 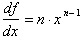 where n is a positive integer. The derivative reflects the instantaneous rate of change of the function at any value x. The derivative is also a function of x whose value is dependenton x.
where n is a positive integer. The derivative reflects the instantaneous rate of change of the function at any value x. The derivative is also a function of x whose value is dependenton x.
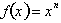 then
then 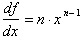 where n is a positive integer. The derivative reflects the instantaneous rate of change of the function at any value x. The derivative is also a function of x whose value is dependenton x.
where n is a positive integer. The derivative reflects the instantaneous rate of change of the function at any value x. The derivative is also a function of x whose value is dependenton x.
Take a look at the left side of the function, 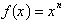 By definition the derivative of a dependent variable, f, is
By definition the derivative of a dependent variable, f, is 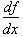 , which is the instantaneous rate of change of f with respect to x at any condition x. The right side of the function,
, which is the instantaneous rate of change of f with respect to x at any condition x. The right side of the function, 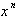 , represents the independent variable whose derivative is
, represents the independent variable whose derivative is 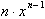
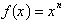 By definition the derivative of a dependent variable, f, is
By definition the derivative of a dependent variable, f, is 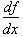 , which is the instantaneous rate of change of f with respect to x at any condition x. The right side of the function,
, which is the instantaneous rate of change of f with respect to x at any condition x. The right side of the function, 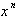 , represents the independent variable whose derivative is
, represents the independent variable whose derivative is 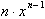
When differentiating a function of the form 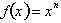 , the derivative of the dependent variable is,
, the derivative of the dependent variable is, 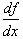 , and the derivative of the independent variable is
, and the derivative of the independent variable is 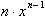 . Thus differentiating a function results in a new function of x, where
. Thus differentiating a function results in a new function of x, where 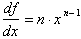 . The derivative is called
. The derivative is called 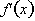 , read “f prime of x”, and it represents the derivative of a function of x with respect to the independent variable, x.. If
, read “f prime of x”, and it represents the derivative of a function of x with respect to the independent variable, x.. If 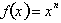 , then:
, then:
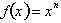 , the derivative of the dependent variable is,
, the derivative of the dependent variable is, 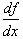 , and the derivative of the independent variable is
, and the derivative of the independent variable is 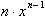 . Thus differentiating a function results in a new function of x, where
. Thus differentiating a function results in a new function of x, where 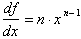 . The derivative is called
. The derivative is called 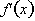 , read “f prime of x”, and it represents the derivative of a function of x with respect to the independent variable, x.. If
, read “f prime of x”, and it represents the derivative of a function of x with respect to the independent variable, x.. If 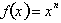 , then:
, then: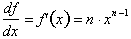
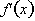 gives the instantaneous rate of change of f(x) as a function of any value, x. Remember that the rate of change of a function other than a line is not constant. Its value changes as x changes.
gives the instantaneous rate of change of f(x) as a function of any value, x. Remember that the rate of change of a function other than a line is not constant. Its value changes as x changes.
If f(x) were equal to a constant multiplied by a function of x such as:
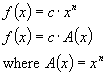
The derivative of f(x) would be:
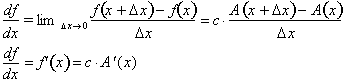
Thus the derivative of f(x) with respect to x, is the constant multiplied by the derivative of the function of x, A(x).
No comments:
Post a Comment